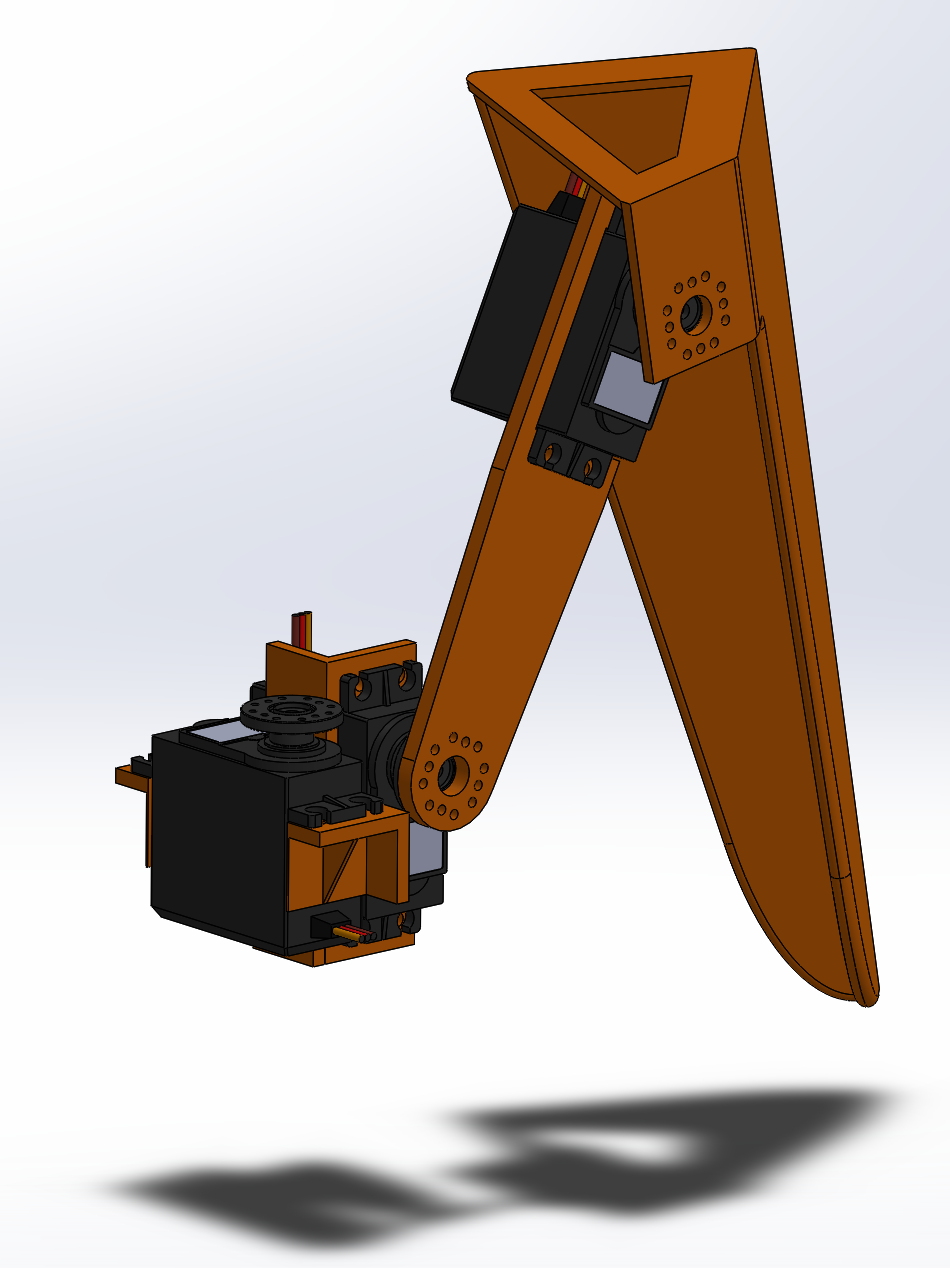
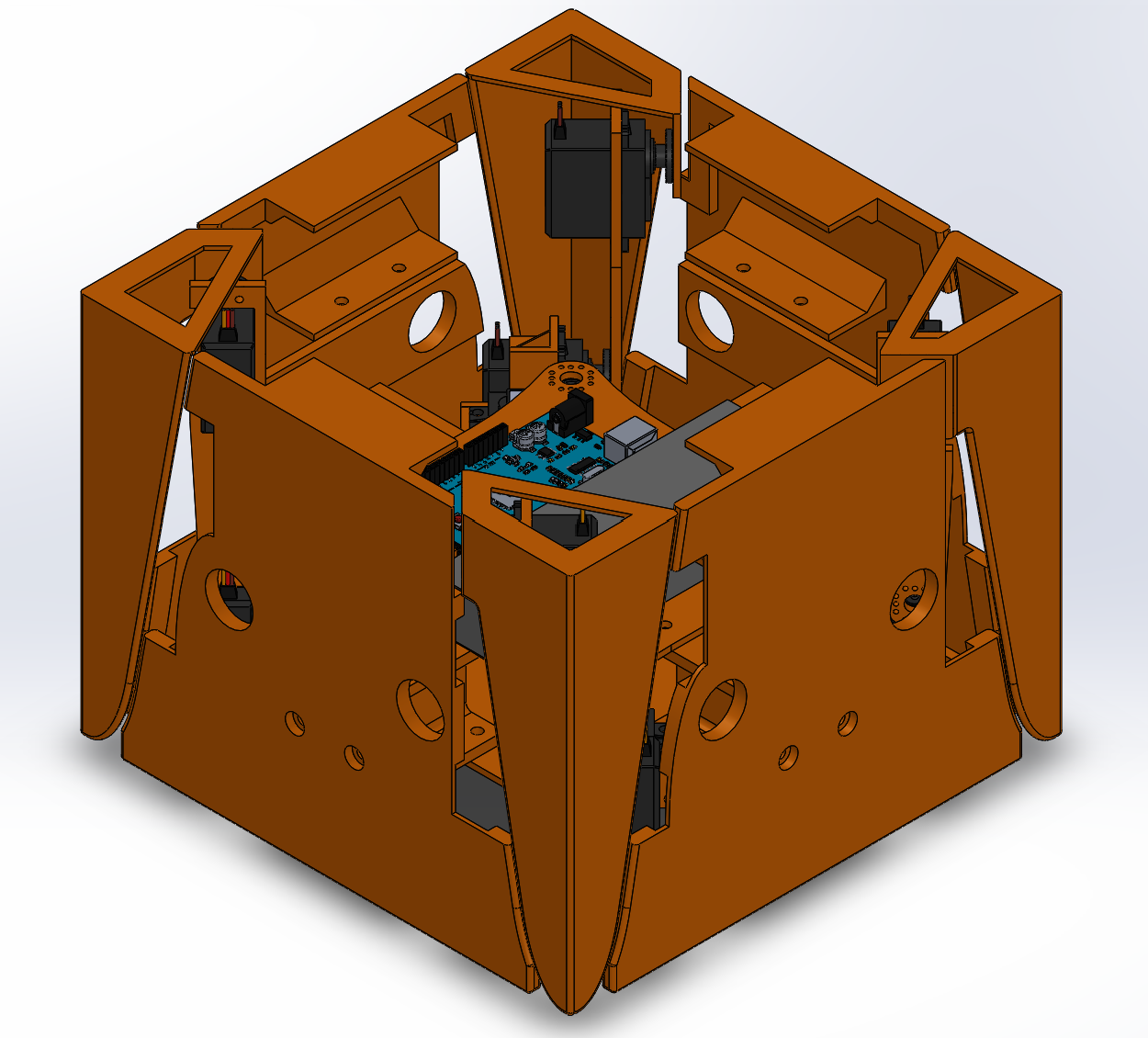
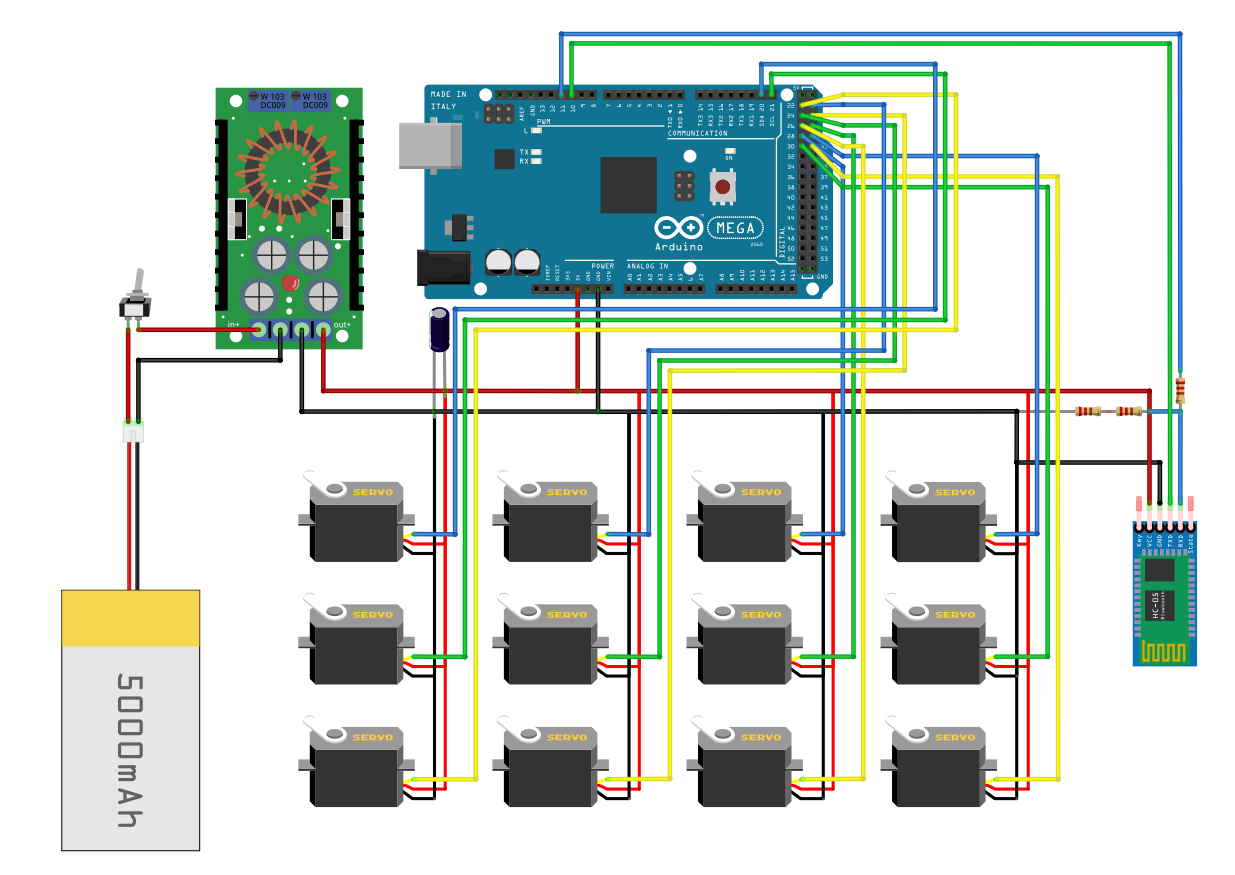
Next, a path is created for the foot to follow. The path is generated
from one of four stride types as defined below:
StrideTypes.MOVE_FORWARD
StrideTypes.MOVE_BACKWARD
StrideTypes.ROTATE_CW
StrideTypes.ROTATE_CCW
The create_foot_path function returns a path represented by lists of
discrete points. These points are defined in rectangular coordinates (x,
y, z) for stride types MOVE_FORWARD and MOVE_BACKWARD, and in
polar coordinates (θ, ρ, z) for stride types ROTATE_CW and ROTATE_CCW.
% Create relative paths
[lift_path, drag_path] = create_foot_path(STRIDE_TYPE, FULL_STRIDE_LENGTH, FULL_STRIDE_ARC_LENGTH,
ROBOT_RADIUS, STEP_HEIGHT, FULL_STRIDE_TIME, TIME_DELTA);
The returned path is divided into two parts, a lift_path and
a drag_path. The lift_path consists of relative
coordinates that move the foot along a parabolic curve in the z direction,
to lift it off the ground and take a step. The drag_path
contains the relative coordinates required to drag the foot along
the ground, which returns the foot back to its original position
and creates the necessary friction to move the robot. Opposite pairs of
feet on the robot alternate between the lift and drag paths, which creates
the overall walking motion.
After calculating the ideal path for each foot to follow, the script
applies an inverse kinematics solver at each point in the path. Inverse
kinematics is the process of computing the joint angles in some chain of
rigid bodies required to place some end effector at a desired position and/
or orientation. In this case, the chain of bodies is the robot leg, the
joints are located at the servo motors, and the end effector is the foot. The
code snippet
which runs the inverse kinematics solver is shown below.
% Inverse Kinematics
q0 = homeConfiguration(robot);
num_dof = length(q0);
num_timesteps_per_path = size(lift_path, 1);
qs = zeros(NUM_CYCLES*2*num_timesteps_per_path, num_dof);
ik = robotics.InverseKinematics('RigidBodyTree', robot);
weights = [0, 0, 0, 1, 1, 1];
for i = 1:NUM_CYCLES
% First half-cycle: lift legs 1 and 3
foot1_start_pos = get_pos(robot, q0, 'foot1');
foot2_start_pos = get_pos(robot, q0, 'foot2');
foot3_start_pos = get_pos(robot, q0, 'foot3');
foot4_start_pos = get_pos(robot, q0, 'foot4');
q_init = q0;
for j = 1:num_timesteps_per_path
% Define destination points for each foot
if STRIDE_TYPE == StrideTypes.MOVE_FORWARD || STRIDE_TYPE == StrideTypes.MOVE_BACKWARD
% Rectangular coordinates
foot1_dest_pos = lift_path(j,:) + foot1_start_pos;
foot2_dest_pos = drag_path(j,:) + foot2_start_pos;
foot3_dest_pos = lift_path(j,:) + foot3_start_pos;
foot4_dest_pos = drag_path(j,:) + foot4_start_pos;
else
% Cylindrical coordinates
foot1_dest_pos = pol_plus_cart(lift_path(j,:), foot1_start_pos);
foot2_dest_pos = pol_plus_cart(drag_path(j,:), foot2_start_pos);
foot3_dest_pos = pol_plus_cart(lift_path(j,:), foot3_start_pos);
foot4_dest_pos = pol_plus_cart(drag_path(j,:), foot4_start_pos);
end
% Run IK for each foot
q_sol1 = ik('foot1', trvec2tform(foot1_dest_pos), weights, q_init); % indices 1:3 are relevant to foot1
q_sol2 = ik('foot2', trvec2tform(foot2_dest_pos), weights, q_init); % indices 4:6 are relevant to foot2
q_sol3 = ik('foot3', trvec2tform(foot3_dest_pos), weights, q_init); % indices 7:9 are relevant to foot3
q_sol4 = ik('foot4', trvec2tform(foot4_dest_pos), weights, q_init); % indices 10:12 are relevant to foot4
% Add solution to the qs solution matrix
q_sol = [q_sol1(1:3), q_sol2(4:6), q_sol3(7:9), q_sol4(10:12)];
idx = 2*num_timesteps_per_path*(i-1)+j;
qs(idx,:) = q_sol;
q_init = q_sol;
end
% Second half-cycle: lift legs 2 and 4
foot1_start_pos = get_pos(robot, q_init, 'foot1');
foot2_start_pos = get_pos(robot, q_init, 'foot2');
foot3_start_pos = get_pos(robot, q_init, 'foot3');
foot4_start_pos = get_pos(robot, q_init, 'foot4');
for j = 1:num_timesteps_per_path
% Define destination points for each foot
if STRIDE_TYPE == StrideTypes.MOVE_FORWARD || STRIDE_TYPE == StrideTypes.MOVE_BACKWARD
% Rectangular coordinates
foot1_dest_pos = drag_path(j,:) + foot1_start_pos;
foot2_dest_pos = lift_path(j,:) + foot2_start_pos;
foot3_dest_pos = drag_path(j,:) + foot3_start_pos;
foot4_dest_pos = lift_path(j,:) + foot4_start_pos;
else
% Cylindrical coordinates
foot1_dest_pos = pol_plus_cart(drag_path(j,:), foot1_start_pos);
foot2_dest_pos = pol_plus_cart(lift_path(j,:), foot2_start_pos);
foot3_dest_pos = pol_plus_cart(drag_path(j,:), foot3_start_pos);
foot4_dest_pos = pol_plus_cart(lift_path(j,:), foot4_start_pos);
end
% Run IK for each foot
q_sol1 = ik('foot1', trvec2tform(foot1_dest_pos), weights, q_init); % indices 1:3 are relevant to foot1
q_sol2 = ik('foot2', trvec2tform(foot2_dest_pos), weights, q_init); % indices 4:6 are relevant to foot2
q_sol3 = ik('foot3', trvec2tform(foot3_dest_pos), weights, q_init); % indices 7:9 are relevant to foot3
q_sol4 = ik('foot4', trvec2tform(foot4_dest_pos), weights, q_init); % indices 10:12 are relevant to foot4
% Add solution to the qs solution matrix
q_sol = [q_sol1(1:3), q_sol2(4:6), q_sol3(7:9), q_sol4(10:12)];
idx = 2*num_timesteps_per_path*(i-1)+j+num_timesteps_per_path;
qs(idx,:) = q_sol;
q_init = q_sol;
end
end
The last section of the script exports the joint angles to a CSV file,
which can then be copied into the code that runs on the Arduino. Some
conversion is required to transform the joint angles from the global
reference frame to the local servo reference frame.
function save_qs_to_file(qs)
% Convert from rad to deg
qs = rad2deg(qs);
% Copy initial angles to the beginning
q_init = qs(end,:);
qs = [q_init; qs];
% Convert to servo angle reference frame
% Set all angles to zero-referenced
qs = qs - qs(1,:);
% Reverse directions of joint angles as needed
qs(:,1) = qs(:,1)*-1;
qs(:,4) = qs(:,4)*-1;
qs(:,7) = qs(:,7)*-1;
qs(:,10) = qs(:,10)*-1;
% Add joint angle offsets
qs(:,1) = qs(:,1)+90;
qs(:,2) = qs(:,2)+90;
qs(:,3) = qs(:,3)+225+q_init(3);
qs(:,4) = qs(:,4)+90;
qs(:,5) = qs(:,5)+90;
qs(:,6) = qs(:,6)+225+q_init(6);
qs(:,7) = qs(:,7)+90;
qs(:,8) = qs(:,8)+90;
qs(:,9) = qs(:,9)+225+q_init(9);
qs(:,10) = qs(:,10)+90;
qs(:,11) = qs(:,11)+90;
qs(:,12) = qs(:,12)+225+q_init(12);
% Round to nearest integer
qs = round(qs);
writematrix(qs, 'temp.csv');
end
The main code that runs on the Arduino is located
here,
and is fairly straightforward. The program initializes all servo angles
to their closed positions, which causes the legs to retract into a box.
The main function then continuously listens for a message over
Bluetooth, which is triggered by a button press from my phone. I'm using an app called
Arduino Bluetooth Control
which I found for free on the Play Store to communicate with my HC-05
device, though there are plenty of other apps out there that can serve
the same purpose.